Introduction

Without diffraction and atmospheric turbulence, ideal telescopes would focus stars to points. However, there would also be a single focal point, plane or surface and everywhere else would be out of focus. Back in the real world, where diffraction, atmospheric turbulence and telescope flaws exist, stars are not imaged as points, but rather as Airy disks or seeing disks that are larger. This leads to a range where focus can be obtained. This range is called depth of focus and is the topic of this document.

We’ll first describe depth of focus in more detail. Afterwards, we’ll derive it mathematically and present an approximation and a simplification based on ideal seeing. We’ll then present data for various telescope configurations and discuss challenges with focusing fast optical systems.

Depth of Focus

Today’s telescopes are generally diffraction limited. This means that defects in design and construction are not the limiting factors in focusing a star to a point. The aperture of a telescope limits its ability to focus a star to a disk smaller than an Airy disk. Due to atmospheric conditions this limit is rarely achieved. Good seeing conditions result in disks as small as 2 arc-seconds (2″) in diameter.

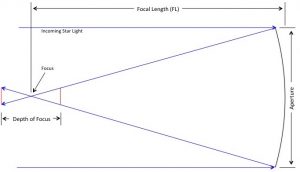
The above figure depicts light from a star entering a reflector telescope from the left and being brought to a focus at the point labelled Focus. As this cone of light converges towards focus, its cross-sectional diameter decreases until focus is reached. Beyond focus its diameter again increases. When the cross-sectional diameter is as small as the Airy disk, or the minimum size disk obtainable due to seeing conditions, there is nothing gained by it being brought closer to the point of focus. The vertical red lines indicate the region within which the image is as small as conditions permit. The length of this region is the depth of focus.

Derivation

The angle, $\theta_{cone}$ , formed by the sides of the cone at the focus, is

$\theta_{cone} = 2 \sin^{-1}(\frac{\text{Aperture}}{2 \times \text{Focal Length}})$

where $\theta_{cone}$ is measured in degrees and the Aperture and Focal Length of the system are measured in meters. Recall that the focal length divided by the aperture of a system is its f-number. Thus,

$\theta_{cone} = 2 \sin^{-1}(\frac{1}{2 \times \text{f-number}})$

As previously mentioned, the cross-sectional diameter of the cone decreases as the focus is approached. We are interested in the distance from the focus to where the cross-sectional diameter of the cone is equal to the diameter of the seeing disk. This is illustrated in the following figure.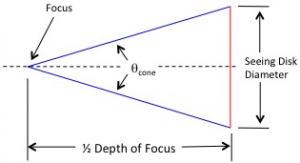The distance from the seeing disk on the right to the focus on the left is,

$\frac{1}{2}F_{depth} = \frac{\frac{1}{2}D_{size}}{\tan \frac{\theta_{cone}}{2}}$

$F_{depth} = \frac{D_{size}}{\tan \frac{\theta_{cone}}{2}}$

where $F_{depth}$ is the depth of focus in meters, $D_{size}$ is the size of the seeing disk in meters and $\theta_{cone}$ is the angle of the converging sides of the light cone at the focus, in degrees.

The size of a seeing disk is described by the following equation.

$D_{size} = \frac{2\pi}{360} \theta_{disk} \times \text{Focal Length}$

where $D_{size}$ is the seeing disk size in meters, $\theta_{disk}$ is the angular size of the seeing disk in degrees, and Focal Length is measured in meters.

Through substitution we obtain the result,

$F_{depth} = \frac{\frac{2\pi}{360} \theta_{disk} \times \text{Focal Length}}{\tan (\sin^{-1}(\frac{1}{2 \times \text{f-number}}))}$

$F_{depth} = \frac{\frac{2\pi}{360} \theta_{disk} \times \text{Focal Length}}{\frac{(\frac{1}{2 \times \text{f-number}})}{\sqrt{1-(\frac{1}{2 \times \text{f-number}})^2}}}$

Approximation

By noticing that the ratio in the denominator of the above equation is approximately equal to $\frac{1}{2 \times \text{f-number}}$ the above equation can be simplified.

$F_{depth} = \frac{\frac{2\pi}{360} \theta_{disk} \times \text{Focal Length}}{\frac{1}{2 \times \text{f-number}}}$

In addition, this result can be simplified and the units of $\theta_{disk}$ can be converted to arc-seconds, to yield,

$F_{depth} = \frac{4\pi}{360} \frac{\theta_{disk}}{3600} \times \frac{(\text{Focal Length})^2}{\text{Aperture}}$

where $F_{depth}$ is the depth of focus in meters, $\theta_{disk}$ is the angular size of the seeing disk in arc-seconds, Focal Length is measured in meters and f-number is the numerical f-number of the system.

Ideal Seeing

Ideally a telescope with an aperture d can focus a star to a seeing disk with an angular diameter of an Airy disk. An approximation for the radius of an Airy disk is given by,

$\theta = 1.22\times\frac{\lambda}{d}$

where $\theta$ is the radius of the Airy disk in radians, $\lambda$ is the wavelength of light in meters and $d$ is the diameter of the mirror or lens in meters. Manipulating this equation to yield a disk diameter in arc-seconds yields,

$\theta = \frac{360}{2\pi} \times 3600 \times 2.44\times\frac{\lambda}{d}$

where $\theta$ is now in arc-seconds and represents the diameter of the Airy disk.

If we adjust $\theta_{disk}$ to be equal to $\theta$ , derived above for the given Aperture d, we obtain,

$F_{depth} = \frac{4\pi}{360} \frac{\frac{360}{2\pi} \times 3600 \times 2.44\times\frac{\lambda}{d}}{3600} \times \frac{(\text{Focal Length})^2}{\text{Aperture}}$

This simplifies quickly to,

$F_{depth} = 2 \times 2.44\times\frac{\lambda}{d} \times \frac{(\text{Focal Length})^2}{\text{Aperture}}$

Recalling that, for this ideal case, we constrained d and Aperture to be equal, this simplifies to,

$F_{depth} = 4.88 \times \lambda \times \text{f-number}^2$

where $\lambda$ is the wavelength of light in meters being observed or imaged and f-number is the numerical f-number of the system. $F_{depth}$ can be adjusted for degraded seeing by multiplying it by the ratio of the width of the seeing disk to the width of the Airy disk for the chosen aperture.

Results

The following table contains depth of focus values in microns for ideal seeing at various f-numbers using the derived equation, the approximate equation and the final equation based on ideal seeing. We’ll assume an aperture of 280mm as two of the three equations require focal length and aperture as parameters. The Airy disk diameter for an aperture of 280mm is 0.97″.

f-number	Actual	Approximate	Ideal
2	10.20	10.53	10.74
3	23.37	23.70	24.16
4	41.81	42.14	42.94
5	65.51	65.84	67.10
6	94.48	94.81	96.62
7	128.71	129.04	131.52
8	168.21	168.54	171.78
9	212.98	213.31	217.40
10	263.02	263.35	268.40

There are two important conclusions that can be drawn from the data in the above table. First, all three of the derived equations yield quite similar results. Second, the fact that the depth of focus is proportional to the square of the f-number is significant. This means that at f/10 the depth of focus is approximately 263 microns while at f/2 it is only about 10.5 microns. It is important to remember that these figures are for seeing disks with a diameter equal to the diameter of the Airy disk. In great seeing conditions where the seeing disk might be 2″, these figures would increase to approximately 543 microns and 21 microns respectively.

For fast telescopes, such as those operating at f/2, the depth of focus is very narrow. These tight tolerances may make focusing these systems a challenge.

Summary

In this post we described depth of focus and derived it mathematically. We then presented an approximation and a model that assumes ideal seeing. The ideal seeing model is routinely used by others and yields good results. Finally, we presented depth of focus figures for various f-numbers and determined that focusing fast optical systems may be problematic.